《算法设计与分析》专题报告
专题名称:蛮力算法的设计与分析
专业:计算机类
班级:22级计算机类二班
学号:XXX
姓名:XXX
指导教师:XX
实验成绩(等级):
日期: 2022 年 9 月 10 日
1、专题名称
蛮力算法的设计与分析
2、实践内容
2.1 实践内容 1
(1)题目要求
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。提示:
2 <= k <= 91 <= n <= 60
(2)算法设计
由题可得,列表不能包含相同的组合两次,若默认k个数由小到大排序,可以减轻计算量。
即问题可转化为k个数的数组之和等于n
其中应满足:
sum[i] < sum[i+1]
sum[i] <= 9
然后再暴力回溯即可
(3)代码实现
class Solution {
public:
/*
sum:数组
now:现在是第几个数
k:一共有几个数
n:k个数之和
*/
vector<vector<int>> result; // 总结果集
void dfs(int *sum,int now,int k,int n)
{
for(int i = sum[now-1]+1 ; i <= 9 ; i++)
{
sum[now] = i;
if(now == k-1) // 如果数量足够
{
int sum_num = 0; // 变量
for(int p = 0 ; p < k ; p++) // 累加数据
sum_num += sum[p];
if(sum_num == n) // 检验输出
{
vector<int> short_result; // 单条式子
for(int p = 0 ; p < k ; p++)
{
short_result.push_back(sum[p]);
}
result.push_back(short_result);
break; // 此时最后一个数字大小已确定,可以直接退出循环
}
continue;
}
dfs(sum,now+1,k,n);
}
}
vector<vector<int>> combinationSum3(int k, int n) {
int sum[9] = {}; // 总和数组
for(int i = 1 ; i <= 9-k+1 ; i++)
{
memset(sum,0,sizeof(sum)); // 重置sum数组
sum[0] = i;
dfs(sum,1,k,n);
}
return result;
}
};(4)算法分析
时间复杂度:O(n^2)
空间复杂度:O(n)
算法优点:实现简单。
缺点:时间复杂度较高。
2.2 实践内容 2
(1)题目要求
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:

输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]示例 2:

输入:head = [1,2]
输出:[2,1]示例 3:
输入:head = []
输出:[]提示:
- 链表中节点的数目范围是
[0, 5000] -5000 <= Node.val <= 5000
(2)算法设计
使用三指针,顺序遍历链表即可,注意对特殊情况的特殊解决方法。
(3)代码实现
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL)
return head;
ListNode* pnow = head; // 现结点指针
ListNode* pfront = pnow->next; // 前结点指针
ListNode* pback = pnow; // 后结点指针
pnow = pnow->next;
while(pfront != NULL)
{
pfront = pfront->next; // 前结点往后移一位
pnow->next = pback; // 现结点的后继结点改为后结点
pback = pnow; // 后结点往后移一位
pnow = pfront; // 现结点往后移一位
}
head->next = NULL; // 反转链表后原来的头结点的后继结点为空
head = pback; // 反转链表后的头结点
return head;
}
};(4)算法分析
时间复杂度:O(n)
空间复杂度:O(1)
算法优点:空间复杂度低。
缺点:稍微难想一点
2.3 实践内容 3
(1)题目要求
给你一份『词汇表』(字符串数组) words 和一张『字母表』(字符串) chars。
假如你可以用 chars 中的『字母』(字符)拼写出 words 中的某个『单词』(字符串),那么我们就认为你掌握了这个单词。
注意:每次拼写(指拼写词汇表中的一个单词)时,chars 中的每个字母都只能用一次。
返回词汇表 words 中你掌握的所有单词的 长度之和。
示例 1:
输入:words = ["cat","bt","hat","tree"], chars = "atach"
输出:6
解释:
可以形成字符串 "cat" 和 "hat",所以答案是 3 + 3 = 6。示例 2:
输入:words = ["hello","world","leetcode"], chars = "welldonehoneyr"
输出:10
解释:
可以形成字符串 "hello" 和 "world",所以答案是 5 + 5 = 10。提示:
1 <= words.length <= 10001 <= words[i].length, chars.length <= 100- 所有字符串中都仅包含小写英文字母
(2)算法设计
1、用两个数组分别计算字母表和单词的单个字母数量
2、遍历词汇表,判断单词的每个字母数量是否小于字母表的每个字母数量,若为真,则计算单词的长度
3、最后输出总单词长度
(3)代码实现
class Solution {
public:
int countCharacters(vector<string>& words, string chars) {
int length_sum = 0; // 输出长度
int letter_sum[26] = {}; // 字母表
for(int i = 0 ; i < chars.length() ; i++)
letter_sum[chars[i] - 'a']++; // 字母表字母数量计算
for(int i = 0 ; i < words.size() ; i++)
{
string str = words[i];
int letter_sum2[26] = {}; // 临时字母表
for(int j = 0 ; j < str.size() ; j++)
letter_sum2[str[j] - 'a']++; // 临时字母表字母数量计算
int num_sum = 0; // 单个单词长度
for(int j = 0 ; j < 26 ; j++)
{
if(letter_sum2[j] > letter_sum[j]) // 如果不符合条件
break;
if(j == 25)
{
for(int k = 0 ; k < 26 ; k++)
{
while(letter_sum2[k]) // 单词长度计算
{
letter_sum2[k]--;
num_sum++;
}
}
length_sum += num_sum;
}
}
}
return length_sum;
}
};(4)算法分析
时间复杂度:O(n)
空间复杂度:O(1)
算法优点:实现简单。
缺点:时间复杂度一般,空间复杂度固定(开两个int类型的长度26的数组),对n小的情况会造成内存浪费。
2.4 实践内容 4
(1)题目要求
给你一个数组 prices ,其中 prices[i] 是商店里第 i 件商品的价格。
商店里正在进行促销活动,如果你要买第 i 件商品,那么你可以得到与 prices[j] 相等的折扣,其中 j 是满足 j > i 且 prices[j] <= prices[i] 的 最小下标 ,如果没有满足条件的 j ,你将没有任何折扣。
请你返回一个数组,数组中第 i 个元素是折扣后你购买商品 i 最终需要支付的价格。
示例 1:
输入:prices = [8,4,6,2,3]
输出:[4,2,4,2,3]
解释:
商品 0 的价格为 price[0]=8 ,你将得到 prices[1]=4 的折扣,所以最终价格为 8 - 4 = 4 。
商品 1 的价格为 price[1]=4 ,你将得到 prices[3]=2 的折扣,所以最终价格为 4 - 2 = 2 。
商品 2 的价格为 price[2]=6 ,你将得到 prices[3]=2 的折扣,所以最终价格为 6 - 2 = 4 。
商品 3 和 4 都没有折扣。示例 2:
输入:prices = [1,2,3,4,5]
输出:[1,2,3,4,5]
解释:在这个例子中,所有商品都没有折扣。示例 3:
输入:prices = [10,1,1,6]
输出:[9,0,1,6]提示:
1 <= prices.length <= 5001 <= prices[i] <= 10^3
(2)算法设计
1、开一个大数组
2、双层for循环,找出符合题目条件的折扣
3、for循环算出最终返回数组
(3)代码实现
class Solution {
public:
vector<int> finalPrices(vector<int>& prices) {
int price_real[500] = {} ;
for(int i = 0 ; i < prices.size() ; i++ )
{
for(int j = i+1 ; j < prices.size() ; j++ )
{
if(prices[j] <= prices[i])
{
price_real[i] = prices[j];
break;
}
}
}
for(int i = 0 ; i < prices.size() ; i++ )
prices[i] -= price_real[i] ;
return prices;
}
};(4)算法分析
时间复杂度:O(n^2)
空间复杂度:O(1)
算法优点:算法易想,实现简单。
缺点:时间复杂度较高,空间复杂度固定(开int类型的长度500的数组),对n小的情况会造成内存浪费。
2.5 实践内容 5
(1)题目要求
超市正在促销,你可以用 numExchange 个空水瓶从超市兑换一瓶水。最开始,你一共购入了 numBottles 瓶水。
如果喝掉了水瓶中的水,那么水瓶就会变成空的。
给你两个整数 numBottles 和 numExchange ,返回你 最多 可以喝到多少瓶水。
示例 1:
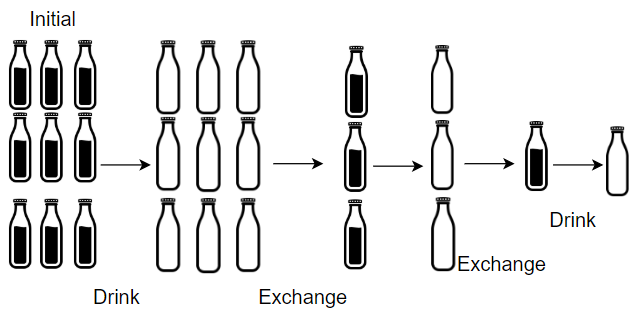
输入:numBottles = 9, numExchange = 3
输出:13
解释:你可以用 3 个空瓶兑换 1 瓶水。
所以最多能喝到 9 + 3 + 1 = 13 瓶水。示例 2:
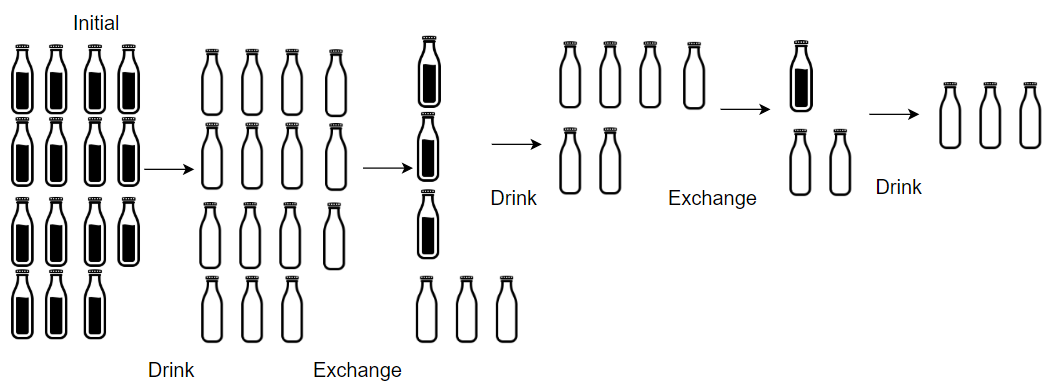
输入:numBottles = 15, numExchange = 4
输出:19
解释:你可以用 4 个空瓶兑换 1 瓶水。
所以最多能喝到 15 + 3 + 1 = 19 瓶水。提示:
1 <= numBottles <= 1002 <= numExchange <= 100
(2)算法设计
while循环对numBottles自减,减够numExchange时再+1即可,同时计算所有喝到的水的瓶数
(3)代码实现
class Solution {
public:
int numWaterBottles(int numBottles, int numExchange) {
int drink = 0;
int total = 0;
while(numBottles)
{
numBottles --;
drink ++;
total ++;
if(total == numExchange)
{
numBottles ++;
total = 0;
}
}
return drink;
}
};(4)算法分析
时间复杂度:O(n)
空间复杂度:O(1)
算法优点:算法易想,实现简单。
缺点:时间复杂度还能进一步优化。
3、问题与总结
问题:第一、第二道题花费时间较长,对力扣的提交模式不熟悉,对C++的容器不熟悉,算法的时间复杂度和空间复杂度不够低。
总结:成功完成所有题目,除第一、二题外,其他题目完成时间短,正确率高。
4、完成情况证明









Comments 2 条评论
请教一下你这个代码块的样式是怎么弄的
@416365641 下了个markdown转换html为的插件,直接用markdown写的文章,代码块就直接markdown语法,最后会自动转成html页面,不需要我操作
(=・ω・=)