回溯算法的设计与分析

singlemouse 发布于 2023-11-08 583 次阅读

Table of Contents

1、专题名称

回溯算法的设计与分析

2、实践内容

2.1 实践内容 1

（1）题目要求

幂集。编写一种方法，返回某集合的所有子集。集合中不包含重复的元素。

说明：解集不能包含重复的子集。

  • 示例:

    输入： nums = [1,2,3]
输出：
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
（2）算法设计

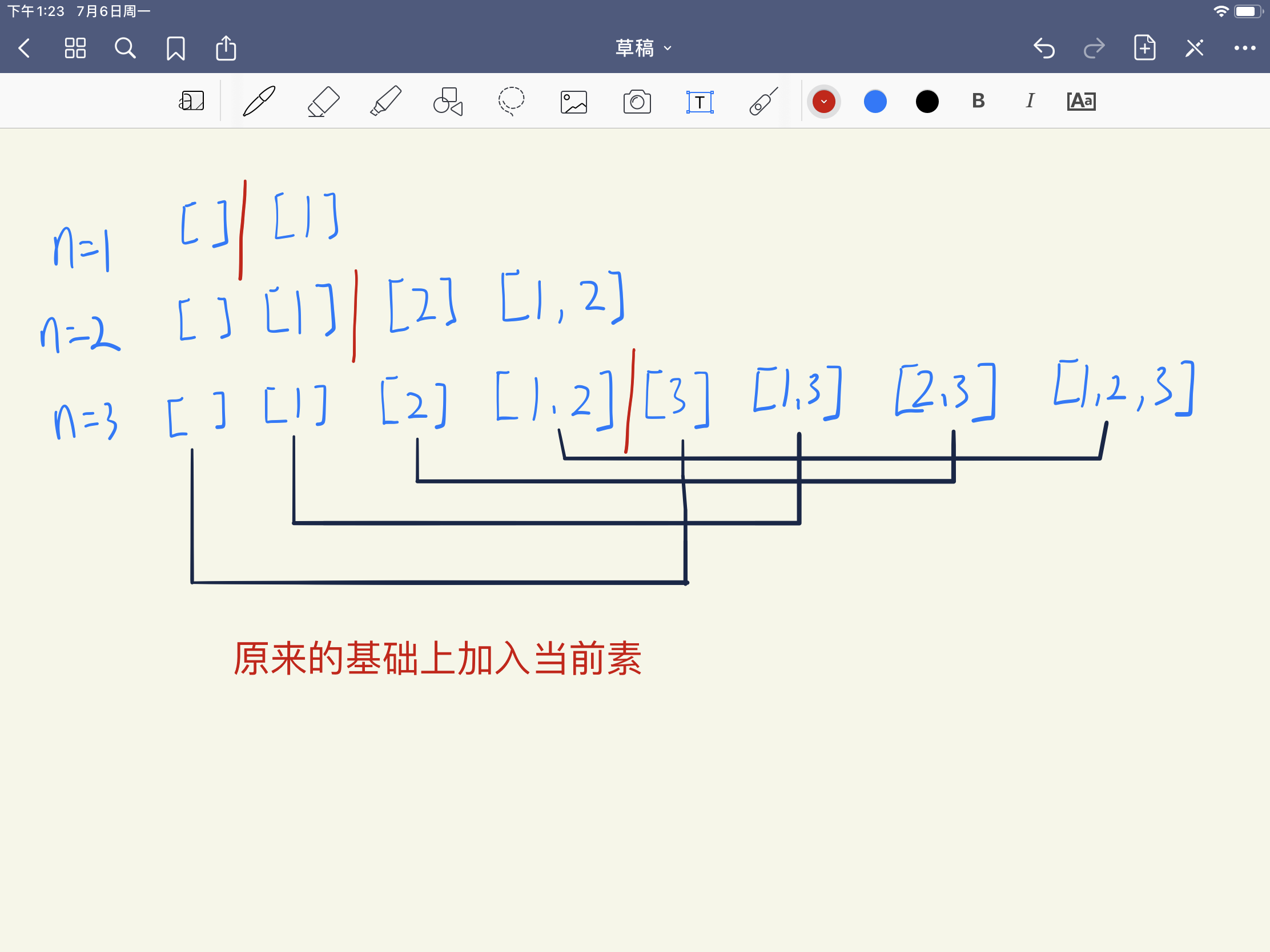
image.png

（3）代码实现
class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>>ans;
        ans.push_back({}); // 默认有个空子集
        for(auto p : nums)
        {
            int n = ans.size(); // 在原有集合的基础上，取出每个集合加上当前元素，然后再加入到集合中
            for(int i = 0 ; i < n ; i++)
            {
                vector<int>temp = ans[i];
                temp.push_back(p);
                ans.push_back(temp);
            }
        }
        return ans;
    }
};
（4）算法分析

时间复杂度：O(n)

空间复杂度：O(1)

算法优点：时间复杂度和空间复杂度都低。

缺点：要把题目转换为数学问题来解决

2.2 实践内容 2

（1）题目要求

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

img

输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

提示：

  • 1 <= n <= 9
（2）算法设计

使用递归遍历每一行，用vector n保存行为i 时的皇后在j列，不能放在斜边：即新的x - y != 已经存在的i - j || (x + y != i + j)

（3）代码实现
lass Solution {
public:
//递归：遍历每一行，用vector<int> n保存行为i 时的皇后在j列，不能放在斜边：即新的x - y != 已经存在的i - j  || (x + y != i + j)
    vector<int> v;
    unordered_map<int, int> m; //保存用过的列
    int ans = 0;
    void dfs(int row, int n) {
        if (row > n) {
            ans++;
            return;
        }

        for (int j = 1; j <= n; j++) { //row行的列
            if (m.find(j) == m.end()) { 
                int condition = 1;
                for (int k = 1; k < row; k++) { 
                    if (k - v[k] == row - j || k + v[k] == row + j) { //验证对角线是否满足条件
                        condition = 0;
                        break;
                    }
                }
                if (condition == 1) {
                    v[row] = j;
                    m[j]++;
                    dfs(row + 1, n);
                    v[row] = 0; // 回溯
                    m.erase(j); // 删除key为j的map?
                }
            }
        }
    }
    int totalNQueens(int n) {
        v.resize(n + 5);
        dfs(1, n);
        return ans;
    }
    //time : n*n* 不过时间复杂度好像不会算...........
    //space : n  疑惑这个哈希表的空间复杂度？
};
（4）算法分析

时间复杂度：O(n^2)

空间复杂度：O(n)

算法优点：空间复杂度低，时间复杂度较低。

缺点：非常难想

2.3 实践内容 3

（1）题目要求
    • 给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

    示例 1：

    输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

    示例 2：

    输入：nums = [0,1]
输出：[[0,1],[1,0]]

    示例 3：

    输入：nums = [1]
输出：[[1]]

    提示：

    • 1 <= nums.length <= 6
    • -10 <= nums[i] <= 10
    • nums 中的所有整数 互不相同
（2）算法设计

比较常规的回溯问题,对特殊情况进行了特殊处理

（3）代码实现
class Solution {
public:
    vector<vector<int>> total;
    void dfs(int now,int sum,vector<int> &past,vector<int> &push,vector<int> &nums){
        for(int i = 0 ; i < sum ; i++){
            int flag = 0;
            if(now == 1 && sum == 1){ // 对只有一个元素的特殊情况 
                past.push_back(i);
                push.push_back(nums[i]);
                total.push_back(push);
                break;
            }
            else{
                for(int j = 0 ; j < past.size() ; j++){
                    if(i == past[j])
                    flag = 1;
                }
                if(flag)
                continue;
            }
            if(now == sum){ // 数组内元素足够
                past.push_back(i);
                push.push_back(nums[i]);
                total.push_back(push);
            }
            else{
                past.push_back(i);
                push.push_back(nums[i]);
                dfs(now+1,sum,past,push,nums);
            }
            if(past.size())
            past.pop_back(); // 删减元素
            if(push.size())
            push.pop_back(); // 删减元素
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        int sum = nums.size(),totalnum = 1;
        vector<int> past;
        vector<int> push;
        dfs(1,sum,past,push,nums);
        return total;
    }
};
（4）算法分析

时间复杂度：O(n!)

空间复杂度：O(n)

算法优点：稍微易想。

缺点：要对C++的容器有一定的了解。

2.4 实践内容 4

（1）题目要求

  • 二进制手表顶部有 4 个 LED 代表 小时（0-11），底部的 6 个 LED 代表 分钟（0-59）。每个 LED 代表一个 0 或 1，最低位在右侧。

    • 例如，下面的二进制手表读取 "4:51" 。

    img

    给你一个整数 turnedOn ，表示当前亮着的 LED 的数量，返回二进制手表可以表示的所有可能时间。你可以 按任意顺序 返回答案。

    小时不会以零开头：

    • 例如，"01:00" 是无效的时间，正确的写法应该是 "1:00" 。

    分钟必须由两位数组成，可能会以零开头：

    • 例如，"10:2" 是无效的时间，正确的写法应该是 "10:02" 。

    示例 1：

    输入：turnedOn = 1
输出：["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"]

    示例 2：

    输入：turnedOn = 9
输出：[]

    提示：

    • 0 <= turnedOn <= 10
（2）算法设计

比较简单的回溯问题,对特殊情况进行处理,用记忆化搜索思想解决

（3）代码实现
class Solution {
public:
    int a[10]={1,2,4,8,1,2,4,8,16,32};
    void dfs(int now,int num,int turnedOn,vector<string> &readBinaryWatch1,bool *b){
        for(int j = now ; j <= 9 ; j++){
            if(9-j+num < turnedOn || num > turnedOn)
            break;
            int flag = 0;
            b[j] = 1;
            int hour = 0;
            int minute = 0;
            for(int i = 0 ; i <= 3 ; i++){
                if(b[i])
                hour+=a[i];
                if(hour >= 12)
                flag = 1;
            }
            for(int i = 4 ; i <= 9 ; i++){
                if(b[i])
                minute+=a[i];
                if(minute >= 60)
                flag = 1;
            }
            if(flag){
                b[j] = 0;
                dfs(j+1,num,turnedOn,readBinaryWatch1,b);
            }
            else if(num == turnedOn){
                string str;
                if(minute < 10)
                str =  to_string(hour) + ":0" + to_string(minute) ;
                else
                str =  to_string(hour) + ":" + to_string(minute) ;
                if(find(readBinaryWatch1.begin(),
                        readBinaryWatch1.end(),str)==readBinaryWatch1.end())
                readBinaryWatch1.push_back(str);
            }
            else{
                dfs(j+1,num+1,turnedOn,readBinaryWatch1,b);
            }
            b[j] = 0;
        }
    }
    vector<string> readBinaryWatch(int turnedOn) {
        bool b[10] = {};
        vector<string> readBinaryWatch1;
        if(turnedOn == 0){
            readBinaryWatch1.push_back("0:00");
            return readBinaryWatch1;
        }
        else{
            dfs(0,1,turnedOn,readBinaryWatch1,b);
            return readBinaryWatch1;
        }
    }
};
（4）算法分析

时间复杂度：O(n!)

空间复杂度：O(n)

算法优点：简单易想。

缺点：空间复杂度和时间复杂度都一般,且需对C++的容器有较好的理解.

2.5 实践内容 5

（1）题目要求

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

  • 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

提示：

  • 1 <= s.length <= 20
  • s 仅由数字组成
（2）算法设计

根据题意,可以把IP地址字符串分为四段,三个小数点,注意特殊情况,三重循环遍历即可

（3）代码实现
#include <iostream>
#include <string>
#include <vector>
using namespace std;

void dfs(vector<string> &strsum,string str){
        for(int i = 1 ; i <= 3 ; i++){
            string comp = "255";
            string s1 = str.substr(0,i-0);
            cout << "s1:" + s1 << endl;
            cout << "i:" + to_string(i) << endl;
            if(s1.length()>1&&s1[0] == '0')
            continue;
            for(int j = i+1 ; j <= i+3 && j < str.length() ; j++){
                string s2 = str.substr(i,j-i);
                cout << "s2:" + s2 << endl;
                cout << "j:" + to_string(j) << endl;
                if(s2.length()>1&&s2[0] == '0')
                continue;
                for(int k = j+1 ; k <= j+3 && k < str.length() ; k++){
                    string str2;
                    string s3 = str.substr(j,k-j);
                    string s4 = str.substr(k,str.length()-k);
                    cout << "s3:" + s3 << endl;
                    cout << "s4:" + s4 << endl;
                    cout << "k:" + to_string(k) << endl;
                    if(s1.length()>2 && s1 > comp || s2.length()>2 && s2 > comp || s3.length()>2 && s3 > comp || s4.length()>2 && s4 > comp)
                    continue;
                    else if(s1.length()>1&&s1[0] == '0' || s2.length()>1&&s2[0] == '0' ||
                        s3.length()>1&&s3[0] == '0' || s4.length()>1&&s4[0] == '0')
                    continue;
                    else if(s1.length()>3 || s2.length()>3 || s3.length()>3 || s4.length()>3)
                    continue;
                    str2 = s1 + "." + s2 + "." + s3 + "." + s4;
                    strsum.push_back(str2);
                }
            }
        }
    }
int main(int argc, char** argv) {
    string s;
    cin >> s;
    vector<string> strsum;
    if(s.length()>12 || s.length()<4);
    else
    dfs(strsum,s);
    for(auto x: strsum)
    cout << x << endl;
    return 0;
}
（4）算法分析

时间复杂度：O(n^3)

空间复杂度：O(n)

算法优点：简单易想。

缺点：空间复杂度和时间复杂度都一般,且需熟悉C++的字符串.

3、问题与总结

问题：以上题目对C++的容器,字符串有较高要求,花了一定时间学习

总结：总体耗时较短，且对C++的容器的使用更加熟练

4、完成情况证明

此作者没有提供个人介绍
最后更新于 2023-11-08
啥也没有呀